New Cryopreservation Technology
October 2005
(see also “M22 Implementation” from Alcor News, Oct. 13, 2005)
Overview
Reversible suspended animation requires successful preservation and recovery of structure and function of an organism, especially the brain. Historically cryonics has focused on preservation of cell structure as revealed by electron microscopy. It was reasoned that if at least structure was well preserved, nanotechnology could reverse chemical changes that caused loss of function. This led Alcor to increase the concentration of glycerol used for freezing during the 1990s, and ultimately to switch to cryoprotectant mixtures capable of vitrification (ice-free preservation) after the turn of the century.
Alcor first implemented vitrification for neuropreservation cases using B2C cryoprotectant solution. It was not possible to immediately extend this technology to whole bodies because B2C could not be perfused into whole bodies without causing tissue swelling, and because the physical apparatus for cooling whole bodies quickly to the required temperature of -120ºC did not exist. Whole body cases therefore continued to be treated with either conventional glycerol cryoprotection and freezing, or by separation of the head for better brain preservation by neurovitrification, and separate freezing of the body. This combination procedure caused much media misunderstanding.
In 2005, Alcor completed construction of a cold nitrogen gas cooling system for attempting vitrification of whole bodies. Also, another cryoprotectant solution suitable for large system vitrification had been validated in brain and whole animal studies. This solution, called M22, did not permit vitrification of all parts of the body because some tissues absorb cryoprotectant too slowly. However it seemed adequate for vitrification of tissues with a rich supply of blood vessels, such as the brain. Therefore it should be possible to vitrify the brain during cryopreservation of the entire body, not just the head. The rest of the body would experience varying degrees of vitrification and freezing during the process, with freezing injury reduced by presence of M22 solution.
This “M22 procedure” is Alcor’s new cryopreservation technology. M22 solution will now be used for both whole body and neuropreservation cases, making B2C obsolete. It also marks an important technology transition as Alcor begins to move beyond just structure preservation toward better preservation of biochemistry and functional capacity. The advantages of M22 over B2C are discussed below.
Solution Comparison
In 2001 Alcor switched from high concentration glycerol to B2C vitrification solution for cryoprotection of neuropatients. B2C is a more concentrated variant of the VM3 vitrification solution used in mainstream cryobiology for vitrification of mouse ova and kidney slices [1]. B2C was designed as a “hyperstable” vitrification solution, meaning that it’s so concentrated that it’s virtually impossible to freeze. This was done to help ensure that Alcor’s first attempts at brain vitrification would be successful, with the understanding the cellular viability by conventional spontaneous recovery criteria would be low to non-existent. Thus the purpose of B2C was to eliminate structural damage from ice under good conditions, not preserve viability by conventional measures.
The composition of B2C is:
|
Dimethyl sulfoxide
|
24.765% w/v
|
| Formamide | 17.836% |
| Ethylene glycol | 17.401% |
| Polyvinyl pyrrolidone K12 | 2% |
| Polyvinyl pyrrolidone K30 | 2% |
| X-1000 ice blocker | 1% |
| Z-1000 ice blocker | 1% |
The solution was prepared in a carrier solution of non-penetrating solutes called B1, similar in composition to the published vitrification carrier solution LM5 [2].
Figures 1 and 2 show electron micrographs prepared from rabbit brains after perfusion with B2C solution in a manner that replicates Alcor’s neurovitrification protocol prior to deep cooling. The micrographs therefore represent the state of the brain immediately prior to deep cooling for vitrification. The second figure is more representative of human cases since the peak concentration phase of perfusions are more likely to last two or more hours rather than the one hour of Fig. 1. Both figures show disturbing structural alterations.

Figure 1. B2C perfusion for one hour at -4ºC (no further cooling). Rabbit hippocampus at 6700x magnification. White holes appear to be shrinkage spaces caused by extreme cellular dehydration. While less damaging than ice, such artifacts are still undesirable. Two opaque black particles on the micrograph are preparation artifacts.

Figure 2. B2C perfusion for two hours at -4ºC (no further cooling). Rabbit cerebral cortex at 8000x magnification. There is less dehydration space than in Fig. 1, but unusually pale cytoplasm and dark chromatin clumping in the central cell. With the exception of the unusual appearance of this cell, other structures appear intact. This type of cell was seen infrequently.
More recent developments in cryobiology offer a better alternative. A new vitrification solution called M22 has been developed by mainstream tissue banking researchers [2]. The published composition is as follows:
|
Dimethyl sulfoxide
|
22.305% w/v
|
| Formamide | 12.858% |
| Ethylene glycol | 16.837% |
| N-methylformamide | 3% |
| 3-methoxy-1,2-propanediol | 4% |
| Polyvinyl pyrrolidone K12 | 2.8% |
| X-1000 ice blocker | 1% |
| Z-1000 ice blocker | 2% |
The solution must also contain non-penetrating solutes of a suitable carrier solution, such as LM5 [2], at isotonic concentration brought to a final pH of 8.
M22 has a critical cooling rate of approximately 0.1ºC per minute, and a critical warming rate of 0.4ºC per minute after rapid cooling. The critical warming rate is approximately 1ºC per minute after slow cooling. This is more than sufficient for structural vitrification of an object the size of the human brain, which can be cooled at 0.4ºC per minute with no near-term need for warming. Figure 3 shows a two liter volume of M22 vitrified by standing in unstirred cold nitrogen for 18 hours.

Figure 3. Two liters (5 pounds) of M22 solution cooled at 0.14ºC/minute (18 hours) until vitrified at a temperature of -124ºC.
Alcor has previously published the results of rabbit brain vitrification with M22 [3]. These results have now been extended to confirm that vitrification still occurs even when cooling at human neuropatient rates. Figures 4 and 5 show electron micrographs of M22-perfused rabbit brains that were cooled at the same rate as the core of an Alcor neuropatient, and subsequently rewarmed as rapidly as possible by forced convection. Both brains successfully vitrified, showing no signs of ice formation. This is very remarkable in the case of Fig 5, for which only 81% of normal M22 solute concentration was used. That concentration of M22 would not remain vitrified if tested as a bare solution, indicating that brain tissue can be more stable against ice formation than the solution it is perfused with (perhaps because of dehydration effects). This is consistent with other studies that show large ice-free areas in brains treated with high concentration glycerol, even though such concentrations of glycerol would not vitrify under ordinary circumstances.

Figure 4. M22 perfusion for one hour at -3ºC followed by vitrification at -125ºC and rewarming. Rabbit hippocampus at 1400x magnification. Structural preservation is good, with greatly reduced dehydration artifacts compared to B2C. The hole at the bottom right is a capillary. Circular mottling is a film processing artifact.
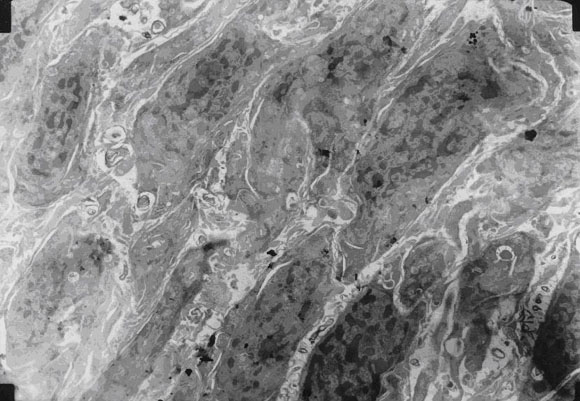
Figure 5. M22 at only 81% full concentration perfused for one hour at -3ºC followed by vitrification at -125ºC and rewarming. Rabbit hippocampus at 1400x magnification. Remarkably, no ice damage was seen anywhere in the brain despite the reduced cryoprotectant concentration. Mottling is chromatin clumping.
The results of Figs. 4 and 5 are also notable because these studies included a proprietary additive to the carrier solution that reduces edema (tissue swelling) in whole body patients. The results of Figs. 4 and 5 can therefore be obtained in both neuro and whole body patients, permitting in-situ brain vitrification of whole body patients without neuroseparation. This was impossible with B2C, which could not be used for whole body perfusions.
Figure 6 shows that perfusion with M22 is compatible with preservation of brain cells even on the synapse level. Similar results were previously obtained with glycerol and cooling in Fig. 3 of this study, but unlike M22, glycerol could not be perfused at concentrations sufficient to prevent ice formation through the entire brain volume.

Figure 6. M22 perfusion for one hour at -3°C (no further cooling). Rabbit brain synapse at high magnification. The synapse and neurotransmitter vesicles remain intact. White spaces are due to dehydration induced by the cryoprotectant.

Figure 7. Suprahippocampal white matter after perfusion with M22 for 60 min at -3°C, cooling to below the glass transition temperature, rewarming, and perfusion fixation. The myelinated fibers are shrunken but intact; lighter spaces are believed to be benign shrinkage spaces. No debris resulting from lysed structures is present. Magnification approximately 5000X on original film.
M22 will be the first solution used in cryonics that preserves both structure and tissue viability under certain circumstances in published studies. In particular, M22 has been used to successfully recover and then transplant whole kidneys after cooling to a temperature of -45 ºC [2]. This success required perfusing M22 at a temperature of -22ºC for only 25 minutes, which is colder and shorter than currently required to prepare a brain for vitrification. So while the same tissue viability seen in published kidney studies cannot be expected in cryonics patients, the use of a solution with such favorable toxicity properties will be less damaging to cell biochemistry than previous solutions used in cryonics.
M22 is less viscous than B2C. Shortened perfusion times will be another advantage of using the solution.
In summary, M22 offers the following advantages:
- Solution of published composition.
- Published success recovering kidneys from -45 ºC.
- Published success at structural brain vitrification.
- Low toxicity per published studies.
- Low viscosity for faster perfusions.
- Compatible with additives permitting whole body perfusion.
References
1. G.M. Fahy, B. Wowk, J. Wu, S. Paynter, Improved vitrification solutions based on the predictability of vitrification solution toxicity, Cryobiology 48 (2004) 22-35. FULL ARTICLE HERE [PDF format].
2. G.M. Fahy, B. Wowk, J. Wu, J. Phan, C. Rasch, A. Chang, E. Zendejas, Cryopreservation of organs by vitrification: perspectives and recent advances, Cryobiology 48 (2004) 157-178. FULL ARTICLE HERE [PDF format].
3. J. Lemler, S.B. Ha/docs/the-arrest-of-biological-time-as-a-bridge-to-engineered-negligible-senescence.pdfrris, C. Platt, T.M. Huffman, The arrest of biological time as a bridge to engineered negligible senescence, Annals of the New York Academy of Sciences 1019 (2004) 559-563. FULL ARTICLE HERE [PDF format] or [HTML format].
